Définition – Généralités
On examine un solide de type poutre en équilibre et on le coupe en deux partie. Afin de reconstituer l’équilibre de la section S, on introduit un effort N , T et un moment Mz. On exprime ainsi les composantes du torseur des forces de qui font venir s’appliquer sur la section S pour rétablir l’équilibre. Dans le cas général nous avons vu (voire articles précédents) qu’il était possible d’exprimer les composantes du torseur des forces de gauche au centre de gravité de la section »S »contenu dans le plan « P ».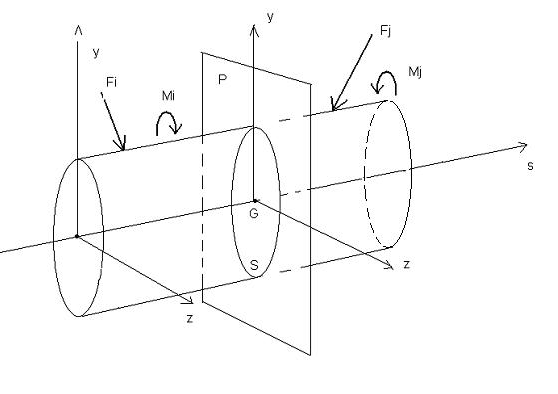
En flexion composée (simple) ces projections ont pour valeurs:
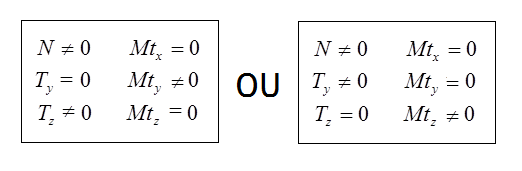
En flexion composée déviée ces valeurs deviennent:
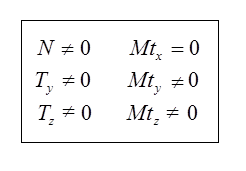
Expression des contraintes normales et déformations
Pour simplifier l’étude nous considérons dans un premier temps le cas de la flexion composée simple avec N,Ty ,et Mtz différent de 0 en prenant par hypothèse des poutres droites à plan moyen chargées dans le plan xGy. Cette hypothèse permet d’exprimer les différentes valeurs dans le système d’axes principal. La poutre offre une section courante »S » N, Ty, Mtz sont appliqués en « G », centre de gravité de « S ».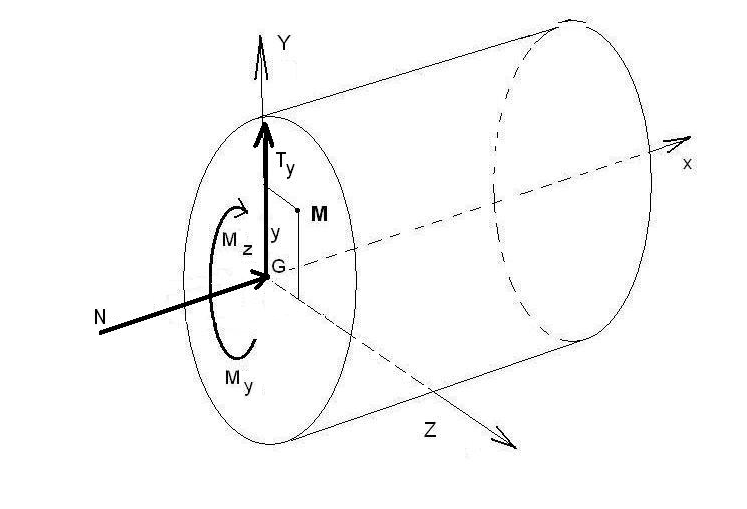
Par application de la loi de Hooke les contraintes normales dues à l’effort normal N, et les contraintes normales dues au moment fléchissant Mtz se cumulent en valeurs algébriques :
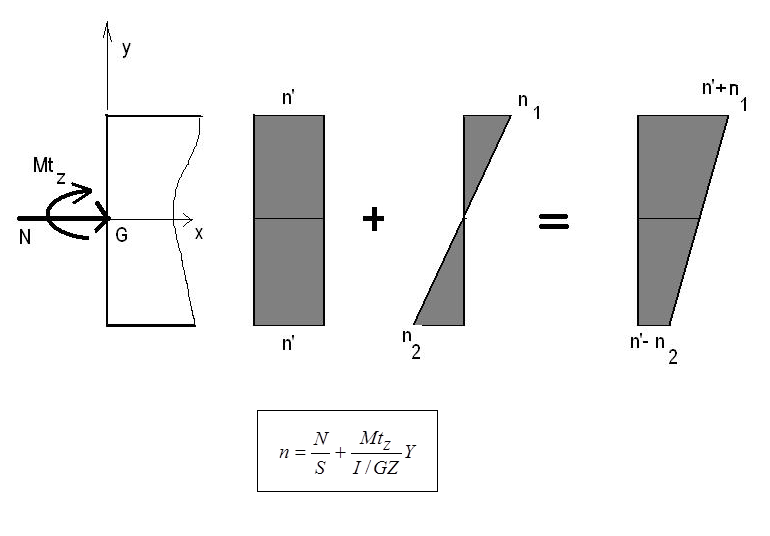
« N » peut être un effort normal de compression ou un effort normal de traction. Dans le cas de la compression un phénomène d’instabilité de forme peut apparaître (risque de flambement) .Ce phénomène fait l’objet d’une étude spécifique dans un second article. L’expérience montre que le risque de flambement apparaît lorsque la longueur de la poutre devient supérieure à 10 fois sa hauteur.
Dans le cas de la flexion composée déviée, l’expression des contraintes devient:
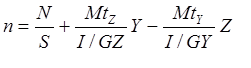
Les contraintes tangentielles dues à Ty ont été étudiées dans un article consacré à l’étude de l’effort tranchant.
Centre de poussée
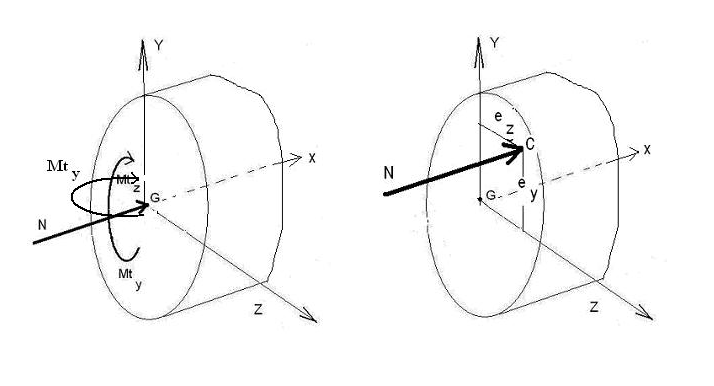
Supposons le système constitué uniquement de N appliqué au point « C ». Exprimons ce système par rapport au point »G ».
N = N M/G = Ney + Nez
Si nous voulons que les 2 systèmes représentés par les figures ci-dessus soient équivalents il faut :
N = N Mtz = Ney et Mty =- Nez
Le point « C » est appelé centre de poussée. Cette notion permet de traduire la flexion composée déviée uniquement en fonction de N.
Axe neutre
L’axe neutre est défini par la famille des points de contraintes normale = 0.
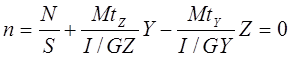
Remplaçons dans cette expression Mtz et Mty respectivement par Ney et – Nez
Or nous avons établi dans le chapitre sur les caractéristiques géométriques des sections:
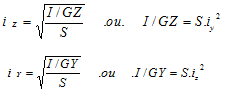
Remplaçons dans l’expression précédente:
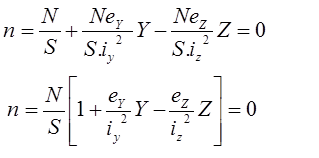
N ≠ 0 et S ≠ 0
La position de l’axe neutre est donc définie par l’expression suivante:
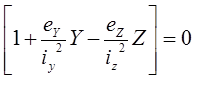
Cette expression représente l’équation d’une droite Y = F ( Z )
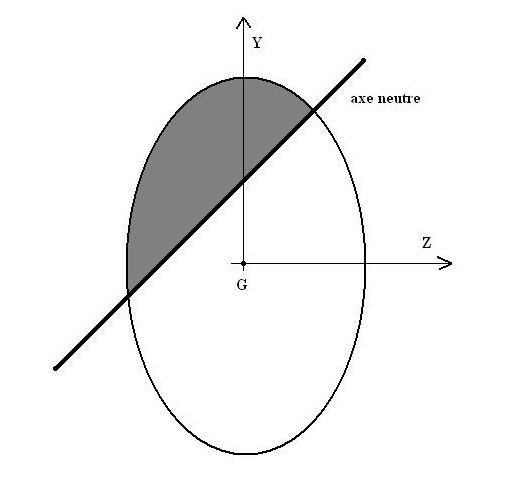
Il faut noter que l’axe neutre ne passe pas par le centre de gravité de la section. L’axe neutre peut se situer en dehors de la section ce qui signifie au sens physique que toute la section est soumise à des contraintes normales de même nature entièrement comprimée ou entièrement tendue.
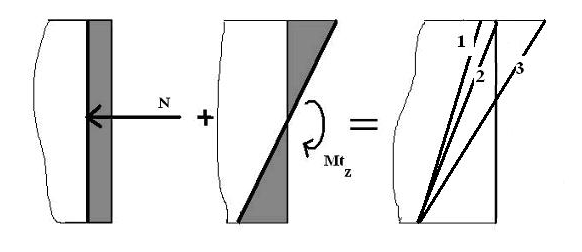
Trois cas peuvent être envisagées :
- la section est entièrement comprimée et l’axe neutre se situe en dehors de la section, ce cas est représenté par la droite (1).
- la section est entièrement comprimée et l’axe neutre se situe juste sur l’extrémité de la section, ce cas est représenté par la ligne (2).
- la section est partiellement comprimée et partiellement tendue, l’axe neutre se situe dans la section, ce cas est représenté par la ligne (3).
Noyau central
Précédemment nous avons vu la flexion composée déviée pouvait s’exprimer dans la section par l’application de N au centre de poussée. D’autre part nous avons vu ,qu’en fonction des valeurs des contraintes normales dues à l’effort normal « N » et des contraintes normales dues aux moments fléchissant MtZ et MtY ,la section » S » pouvait être entièrement soumise à une contrainte de même nature ou partiellement comprimée et tendue. Cherchons à définir l’espace représenté par la famille des points « C » tel que la section soit soumise à une contrainte unique (entièrement comprimée ou entièrement tendue). Cet espace, par définition, est appelé » Noyau central « . Si l’on suppose cet espace connu pour une section donnée , on pourra dire que si N est appliqué dans cet espace alors toute la section est soit comprimée soit tendue.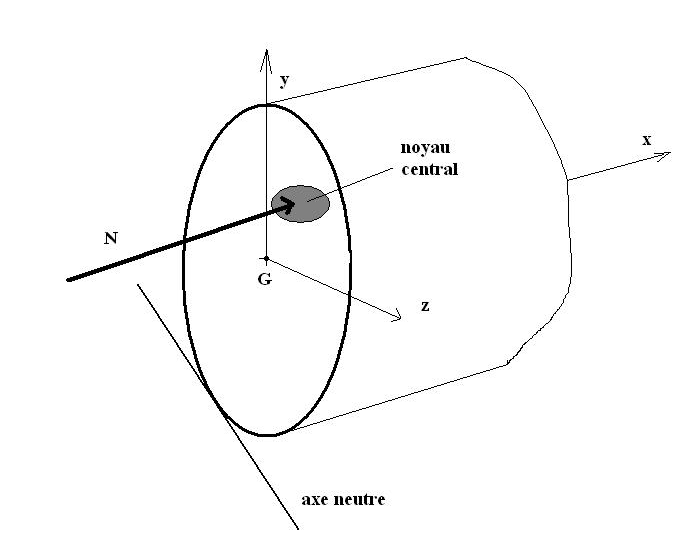
Exercice 1
Soit une poutre de section rectangulaire, cherchons à définir le noyau central.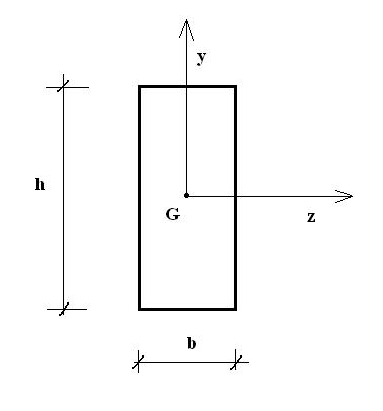
Nous avons établi précédemment l’expression de la contrainte « n » en fonction de N, Mty, Mtz
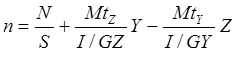
Dans cette expression Z ,Y représentent les coordonnées du point « M » sur lequel nous évaluons la somme des contraintes normales dues à N, Mtz, Mty. Dans une section donnée les valeurs géométriques sont constantes.
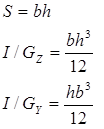
Par définition « N « est constant dans S. Nous avons établi précédemment MtZ = NeY et MtY = NeZ Remplaçons l’ensemble de ces valeurs dans l’équation de » n « .
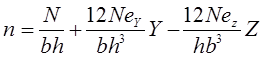
Pour définir le noyau central il faut donc faire varier eY et eZ de tel manière que la contrainte « n » sur la totalité de S soit de même signe, par exemple >0.
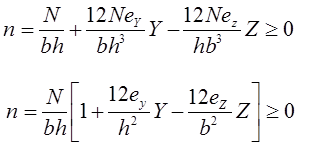
D’autre part les contraintes normales dues aux moments sont maximales pour les valeurs extrêmes de Y et Z. 4 cas sont donc à considérer :
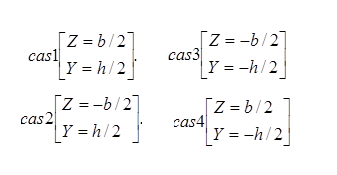
Il faut donc résoudre 4 inéquations du 1 er degrés.
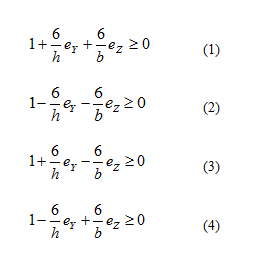
Ces 4 inéquations représentent des droites du type eY = f( eZ )
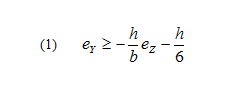
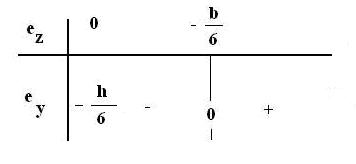
Représentons le tableau de variation de eY
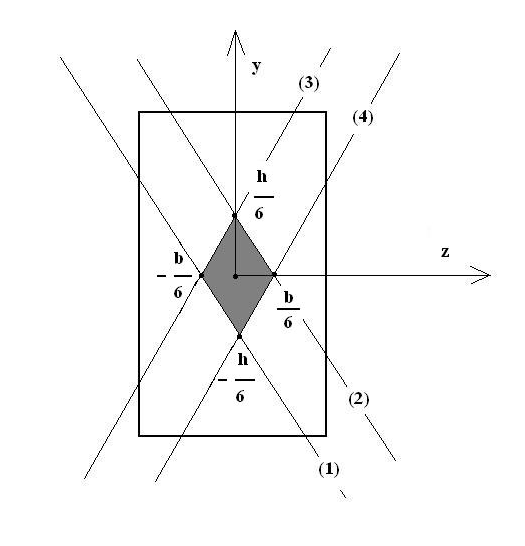
Il successivement étudier de la même manière les 3 autres inéquations puis représenter les 4 droites sur la section afin de déterminer les zones positives. En définitif l’intersection des 4 conditions permet de déterminer une zone géographique qui correspond à un losange de largeur b/3 et de hauteur h/3.
Exercice 2
Soit une section circulaire de grand diamètre « D » soumise à N et MtZ . Déterminer la forme du noyau central.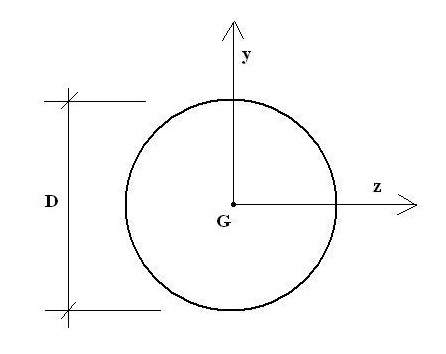
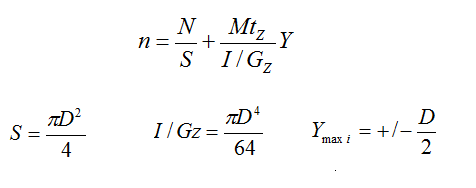
En remplaçant ces valeurs dans l’expression de « n » on obtient:
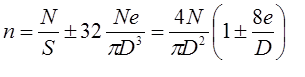
La section est entièrement comprimée si les 2 conditions suivantes sont satisfaites:
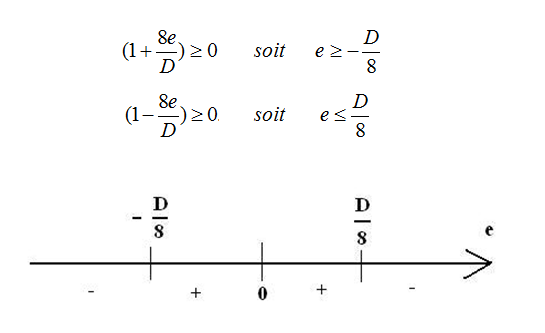
Le noyau central est donc défini par un cercle de diamètre D/8.
Exercice 3
Soit une section annulaire de diamètre extérieur D et diamètre intérieur d. Cette section est soumise à N MtZ.. Déterminer le noyau central.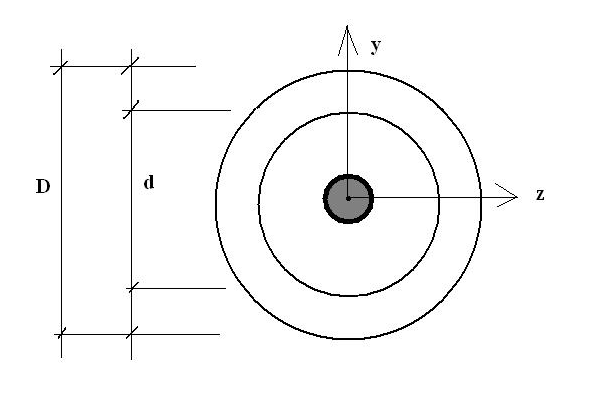
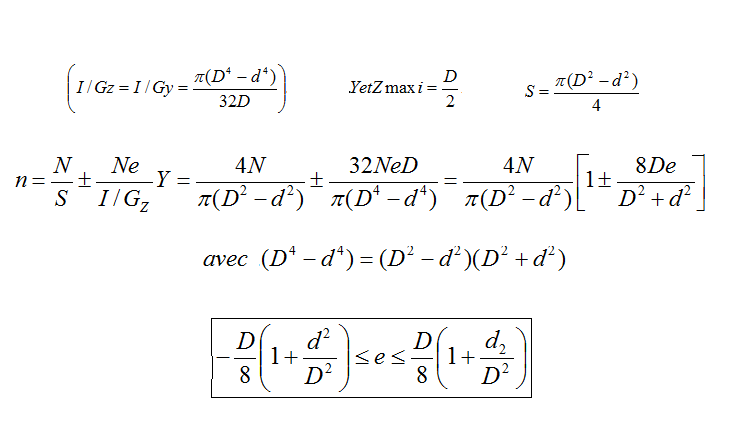








0 commentaires:
Enregistrer un commentaire