1/ Introduction
Rappel et mise au point
En
topographie, les angles sont observés et mesurés dans le sens topographique ou
sens des aiguilles d'une montre. L'unité angulaire employée est le grade et a
pour symbole gon (du grec gônia).
En guise de rappel, le tableau suivant reprend les unités officielles de
longueurs et de surfaces employées en topographie :
Grandeur
|
Unité
|
Symbole
|
Distance
|
Mètre
|
m et km
|
Angle
|
Grade
|
gon ,mgon et dmgon
|
radian
|
rad ,mrad
|
|
Surface
|
Mètre carré
|
m²
|
Surface agraire
|
are
|
a ,ca et ha
|
* Le grade (ou
gon) est l'angle au centre qui intercepte sur la circonférence un arc d'une
longueur égale à 1/400 de celle de cette circonférence.
La conversion radians - grades
s'exprime par la relation :

Avec
2π = 400gon
Relation entre les unités de mesure des
angles
2/ Résolution de triangles
La
trigonométrie constituant la base des calculs topographiques, il est utile de
savoir calculer les paramètres définissant la figure élémentaire de base qu'est
le triangle. Ce paragraphe rappelle quelques formules simples issues de la
trigonométrie dans le plan.

a, b, c : longueurs des côtés opposés aux sommets
A, B, C du
triangle quelconque ABC
A', B', C' :
angles aux sommets A, B, C du triangle
quelconque
ABC
Suivant les
données dont on dispose, le calcul des inconnues du triangle se calculent à
l'aide des formules présentées dans le tableau ci-dessous :
 |
Formulaires servant aux calculs des résolutions des triangles |
3/ Système de projection Lambert
La
plupart des cartes topographiques employées en France (et par conséquent au
Maroc) ont été élaborées suivant la projection conique conforme de Lambert.
Nous retiendrons que cette projection projette, d'une part, les méridiens selon
des droites concourantes présentant un angle Gamma (appelé "convergence
des méridiens") et d'autre part les parallèles selon des cercles
concentriques (projection "conique"). Elle a pour caractéristique de
conserver les angles (projection "conforme").
 |
Système Lambert Maroc |
Avant
d'aborder le calcul de coordonnées dans le plan, nous rappelons la définition
des coordonnées d'un point M quelconque suivant le système d'axes
employé :
 |
Systèmes de coordonnées planes |
4/ Calcul d'un gisement :
On appelle gisement d'une direction orientée AB, l'angle orienté que
fait cette direction avec l'axe parallèle à l'axe des ordonnées, pris pour
origine du quadrillage et orienté du sud vers le nord. Les gisements sont
comptés positivement de 0 à 400 gon dans le sens de la marche des aiguilles
d'une montre (sens topographique). La figure ci-après présente en rouge le
gisement de la droite AB.
 |
Gisement d'une droite AB |
Le gisement
d'une droite AB se calcule à l'aide des coordonnées des points A et B de la
manière suivante :

Dans ce calcul
d'arc (arctan) compris entre 0 et 400 gon, il faut considérer 2 valeurs possibles
pour l'angle considéré car GAB=GAB+ou-
200.
La valeur du gisement va dépendre du signe du numérateur et du
dénominateur, c'est pourquoi, avant tout calcul de gisement, il sera nécessaire
d'effectuer les tests suivants :
 | |
|
Une
autre méthode consiste à calculer le gisement par conversion d'angle
rectangulaire/polaire. Néanmoins, pour des raisons de confort de calculs, il
est conseillé d'adopter la première méthode. La revue Géomatique Expert - n°7
- septembre 2000 présente encore
d'autres méthodes de calcul du gisement.
5/ Calcul d'un point lancé :
Lorsque
les coordonnées d'une extrémité A d'un segment ainsi que son gisement et sa longueur
sont connus, il est aisé de calculer les coordonnées de l'autre extrémité B par point lancé.

6/ Transmission
de gisements :
Avant
d'aborder la transmission de gisements, il est utile de détailler l'expression
des gisements lorsque la droite orientée change de sens et lorsqu'elle subit
une rotation.
Changement
de sens :

Rotation
directe :

Calcul
d'un angle :

Calcul
d'une transmission de gisements :
À l'aide des relations précédentes, nous pouvons exprimer dans un
cheminement polygonal orienté de 1 vers n, le gisement d'arrivée en fonction du
gisement de départ.

Intersection de droites
Le
calcul des coordonnées d'un point défini par l'intersection de 2 droites peut
être réalisé
par résolution du système d'équation des deux droites, ou par résolution de triangles, ou encore, comme
nous allons le voir, à partir des gisements des droites.
On
connaît les points A et B par leurs coordonnées et les gisements GAM et GBM vers le point
M. On recherche les coordonnées EM et NM du
point M à partir de ces données.
Les calculs sont les suivants :

7/ Changement
de repère (système d'axes rectangulaires plans) Principe :
On connaît les
coordonnées du point M dans le système de coordonnées rectangulaires planes
(E,N). Afin de déterminer ses coordonnées dans un autre système de coordonnées,
on opère un changement de repère. Par exemple, la digitalisation d'une
carte, se fait tout d'abord dans le système de coordonnées relatif à la table à
digitaliser. Afin d'accéder aux coordonnées des points dans un autre système,
il est nécessaire de réaliser un changement de repère.

8/
Expression des transformations directe et inverse
:
Les formules
permettant d'un passer d'un système à l'autre sont les suivantes :

9/ Calcul de
relèvement :
Le relèvement correspond
à une situation de levé, lors duquel il est nécessaire de stationner un
point inconnu en coordonnées. Et afin que ce point soit calculable, il est nécessaire de
viser au moins 3 points d'appuis.
D'un point de
vue gémétrique, le relèvement est une intersection de 2 arcs capables. Plusieurs
solutions de calculs de relèvement existent, qu'elles soient géométriques ou analytiques.
Pour des raisons de simplification de calculs, nous n'aborderons ici que la solution analytique de relèvement
simple selon Delambre.

Considérons
M comme intersection de droites (AM) et (BM) et de (AM) et (CM). Sachant
calculer un point par intersection de 2 droites, il nous est possible d'exprimer la distance
AM
à partir de l'intersection des droites (AM) et (BM), puis cette même distance à
partir des droites (AM) et (CM). Ainsi, en vérifiant l'égalité des deux
expressions de AM et après simplification, nous en déduisons les relations
suivantes :
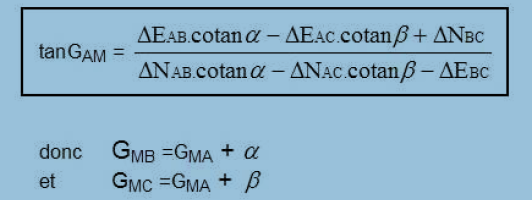








Bonjour, je reconnais des extraits de mon cours de Topométrie dispensé à l'INSA Strasbourg. Je vous prierai de bien vouloir indiquer la source des figures et des captures d'écran, svp, avec la mention "Extrait du support de cours dispensé à l'INSA Strasbourg, spécialité Topographie" ou bien de retirer ce cours de ce site internet.
RépondreSupprimer