Topographie - Généralité suite (3, 4, 5)

3. Coordonnées géographiques, azimut.

Le point B de la terre (fig. 1) se situe grâce à ses coordonnées géographiques, à savoir :

1° Sa longitude, qui est l'angle M formé par le méridien du lieu PBP' avec

un méridien choisi arbitrairement pour origine PGP' (méridien passant par Greenwich). La longitude se compte positivement vers l'ouest (sens des aiguilles d'une montre) et négativement vers l'est.

2° Sa latitude, qui est l'angle L(BOb) du rayon OB avec le plan de l'équateur.

La latitude est aussi, en un lieu, l'angle de hauteur du pôle au-dessus de l'horizon. La colatitude λ est l'arc complémentaire BP. La latitude se compte à partir de l'équateur, soit vers le nord (latitude boréale), soit vers le sud (latitude australe). Le parallèle de B est le petit cercle de la sphère situé dans un plan perpendiculaire à la ligne des pôles et passant par B.

L'azimut d'une direction BC (fig. 2), BC étant une ligne droite sur la terre (appelée géodésique), est l'angle A mesuré au point B dans un plan horizontal, entre la direction du nord (BP) et la direction considérée (BC). Cet angle se mesure dans le sens des aiguilles d'une montre, à partir du nord.

4. Coordonnées rectangulaires et représentation plane de la surface terrestre.

En topographie, on considère la surface de la terre, objet du levé, comme plane. On ne commet, de ce fait, aucune erreur appréciable si la surface levée est relativement réduite.

L'hypothèse ne serait plus valable pour la répertoire étendu. En effet, pas plus qu'on ne peut parvenir à étendre sur une table une écorce d'orange sans la déchirer, on ne peut représenter une fraction importante du globe sans déformer les distances et les angles. Dans ce cas, on a recours à une représentation conventionnelle dite « projection » (projection Lambert, projection de Mercator, projection de Bonne, etc..) dans laquelle les méridiens et les parallèles sont des courbes ou des droites.

La figure 3 représente schématiquement une projection Lambert. Cette projection, comme la plupart, n'est pas une représentation géométrique simple, mais seulement analytique. Cette projection Lambert est particulièrement propre à la représentation d'un pays plus étendu en longitude qu'en latitude; c'est pourquoi la France est couverte par trois systèmes de projection Lambert, dits Lambert nord, Lambert centre et Lambert sud. Un quatrième système est spécial pour la Corse.

Le principe du système Lambert est le suivant : Sur la surface de la terre, dont la forme est sensiblement celle d'un ellipsoïde (fig. 3), on fait choix d'un méridien origine OP (celui de Paris) et d'un parallèle origine OB, tel que 0 soit au centre de la région à représenter.

La fraction de la surface terrestre avoisinant le point 0 sera représentée en plan, dans, un système de coordonnées rectangulaires XOY (fig. 4), d'après les conventions suivantes (à l'échelle de la carte près) :

1° Les méridiens sont représentés par des droites concourantes en p;

2° Les parallèles sont représentés par des cercles concentriques ayant p pour centre;

3° Les longueurs mesurées sur la terre sont conservées sur le parallèle origine.

On conçoit qu'en un point quelconque, tel que a, la direction du nord géographique, représentée par ap, ne soit pas parallèle à l'axe OY.

Coordonnées cartésiennes et polaires

L'angle de ces deux directions est ce que l'on dénomme vulgairement la « déclinaison Lambert ». Sur ce système de projection, on observe des déformations de longueur d'autant plus fortes que l'on s'éloigne du parallèle origine. Toutefois, étant données les origines choisies et l'extension des systèmes, ces déformations de longueur n'ont pas d'influence sensible pour la topographie ou la géométrie, dans une région déterminée.

L'intérêt de ce système est qu'il est « conforme », c'est-à-dire qu'il conserve les angles mesurés sur le terrain, dans la représentation plane, à condition, toutefois, que les longueurs des côtés de ces angles soient petites (par exemple inférieures à 10 km).

Un arrêté interministériel du 10 novembre 1943 prévoit que toutes les opérations topographiques importantes effectuées en France pour les collectivités publiques devront obligatoirement être rattachées et calculées en coordonnées Lambert.

Pratiquement, pour les levés topographiques de surface limitée (inscrits par exemple dans un cercle de 20 km de rayon), on peut considérer la terre comme plate, sans se soucier des théories qui précèdent.

Le fait de se rattacher aux coordonnées Lambert précédemment définies et fournies par l'Institut Géographique National, ne créera aucune difficulté particulière et tout se passera comme si nous travaillions en coordonnées rectangulaires planes de système XOY.

5. Définition de certains termes topographiques.

Établir un plan topographique, c'est représenter à une échelle réduite l'ensemble des détails du terrain projetés verticalement sur la surface horizontale de référence qui est le niveau moyen des mers. Le rapport constant, dans les mesures faites sur le plan, entre la représentation de certains objets et les mesures réelles faites entre ces objets mêmes de la nature, est appelé échelle du plan. Ainsi, par exemple, sur un plan :

au 1/100, 1 mm représente 0,10 m;

au 1/500, 1 mm — 0,50 m;

au 1/1 000, 1 mm — 1 m;

au 1/2 000, 1 mm — 2 m.

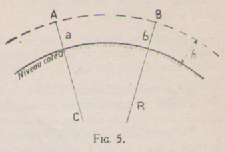
Des définitions qui précèdent, il résulte que le rapport constant ou échelle du plan est valable pour des mesures faites sur le niveau de cote 0 (fig. 5). En d'autres termes,0 une mesure de longueur faite entre A et B à une altitude moyenne h au-dessus du niveau de référence, doit être ramenée à la distance ab des points d'intersection des verticales de A et B avec une surface de référence :

La correction qui en résulte est de l'ordre de 0,16 m pour une mesure de 1 km à l'altitude de 1 000 m. Elle est donc très petite et le plus souvent négligeable pour l'exécution d'un travail à une altitude moyenne. Cette correction s'introduit lors des mesures d'étalonnage des appareils de mesures.

Les détails des accidents topographiques représentés, comme il vient d'être décrit, sont de deux natures : ou ils représentent les contours des objets du sol, tels que routes, chemins de fer, canaux, constructions, cours d'eau, lacs, bois, carrières, limites de propriétés, etc., et se dénomment la planimétrie, ou ils représentent le relief du sol et sont appelés altimétrie.

Le plan planimétrique est toujours une représentation fidèle des objets du sol à l'échelle exacte du plan lorsque l'on fait de la topographie à très grande échelle. Il n'en est pas de même dans les cartes aux petites échelles, car alors les détails à représenter sont trop petits s'ils sont figurés à l'échelle réelle, aussi sont-ils déformés et représentés sous forme de signes conventionnels. C'est là l'une des différences majeures qui existent entre les plans à grande échelle et la cartographie.

L'altimétrie ou relief du sol se représente suivant des conventions diverses qui méritent une étude particulièrement détaillée.